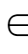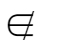1 等式
在上一节中,我们表示两个集合相等时用到的符号“=”,叫做等号(equals sign)。在数学中,我们更多的时候用等号把两个数量连接起来,这样的式子叫做等式(equation)。数量由数字和单位名称组成,在数学上经常把单位抽象为“1”,此时单位可以省略。
或许这个也是等式
例1 列举几个常见的等式。
答:(1)1米=3尺;
(2)1公亩=15亩;
(3)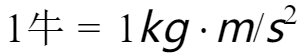 ;
;
(4)1打=12个。
(5)1万=1 0000。
等式具有以下性质:
(1)自环性,任意一个数量等于它本身:a=a;
(2)对称性,等式两边可以互换:若a=b,则b=a;
(3)传递性,等式两边可以通过相等的中间项相互关联:若a=b,b=c,则a=c。
鉴于传递性,我们可以将一系列相等的数量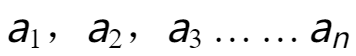 用“=”连接起来,记作:
用“=”连接起来,记作:
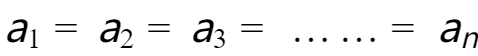
比如:1吨=1000千克=1百万克=2000斤=2万两。
对等式的否定,我们使用“≠”。容易证明,用“≠”连接的式子具有对称性,即:若a≠b,则b≠a。但不具有自环性或传递性。
2映射
对于两个非空集合A、B,如果存在一种对应关系f,而且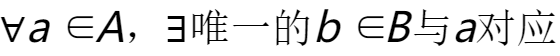 ,记作
,记作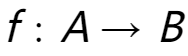 ,我们称f是从A到B的映射(map)。其中,b称为元素a在映射f下的象(image),记作
,我们称f是从A到B的映射(map)。其中,b称为元素a在映射f下的象(image),记作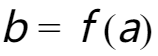 。a称为b关于映射f的象源(preimage)。集合A中所有元素的象的集合称为映射的值域(range),记作
。a称为b关于映射f的象源(preimage)。集合A中所有元素的象的集合称为映射的值域(range),记作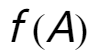 。
。
根据等式的定义和映射的性质,我们可以得到一个应用很广的性质:对于映射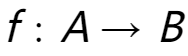 ,若
,若 ,则
,则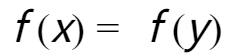 。
。
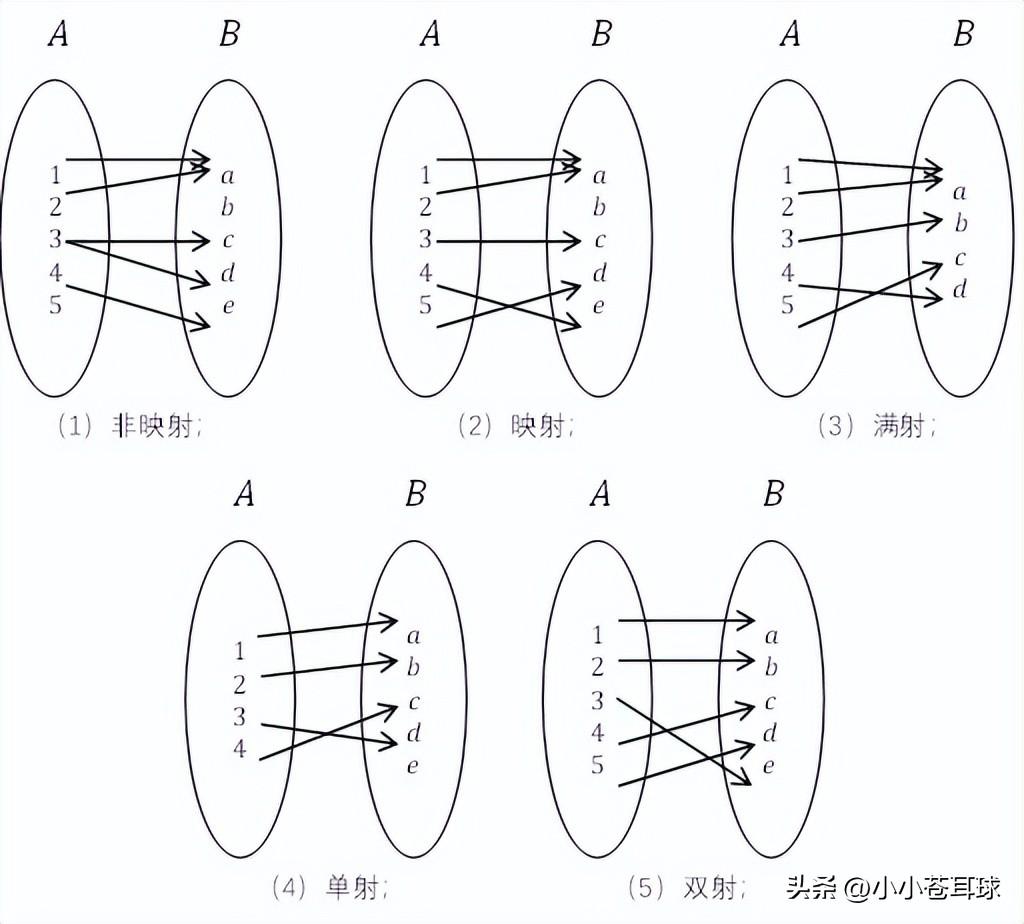
映射
观察图1(1)由于A中元素3对应了B中两个元素,而元素5没有对应的象,所以它不是映射。
如图1所示,对于映射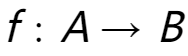 ,若
,若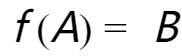 ,则称f是从A到B的满射(surjection);若
,则称f是从A到B的满射(surjection);若 ,则称f是从A到B的单射(injection);若f既是满射又是单射,则称为双射(bijection)。
,则称f是从A到B的单射(injection);若f既是满射又是单射,则称为双射(bijection)。
映射的概念在很多特定的数学领域的底层逻辑中都有应用,在接下来建立自然数集就要用到。
1.3.3 关系符号
像“=”、“≠”一样,表示事物与事物之间某种关系的符号叫做关系符号(relational symbol)。在上一节中,我们用到的 等符号也是关系符号,今后还会遇到更多的关系符号。它们有些也具有“=”类似的性质,具体如表1.3.1。
等符号也是关系符号,今后还会遇到更多的关系符号。它们有些也具有“=”类似的性质,具体如表1.3.1。
表1 关系符号的性质
符号 | 名称 | 自环性 | 对称性 | 传递性 |
= | 等于 | √ | √ | √ |
≠ | 不等于 | × | √ | × |
| 属于 | × | × | × |
| 不属于 | × | × | × |
| 包含(于) | √ | × | √ |
| 不包含(于) | × | × | × |
| 真包含(于) | × | √ | √ |
>、< | 大(小)于 | × | × | √ |
≥、≤ | 不小(大)于 | √ | × | √ |
≈ | 约等于 | √ | × | × |
∝ | 正比于 | √ | √ | √ |
| | 整除 | √ | × | √ |
∤ | 不整除 | × | × | × |
⊥ | 垂直于 | × | √ | × |
∥ | 平行于 | × | √ | √ |
≌ | 全等于 | √ | √ | √ |
∽ | 相似于 | √ | √ | √ |
⇒、⇐ | 推导出 | √ | × | √ |
⇔ | 等价于 | √ | √ | √ |

苍耳球